[java] HashMap 동작 과정, String의 해쉬 값

HashMap

- HashTable과 다르게 쓰레드 동기화를 하지 않음(single-thread에서 유용)

- 기본적으로 해쉬값을 반환하는 해쉬함스로써 hashCode()를 사용함

- hashCode()의 반환형은 int임

- int는 32비트(4Byte)이고 2^32개로 완벽한 해쉬값을 만들 수 없음(표현해야 할 key가 2^32개 보다 많을 경우)

- HashMap은 O(1)을 보장하기 위해 random access가 가능하게 하려면 HashMap의 크기는 2^32개 여야 함

- 그래서 보통 2^32보다 작은 숫자 M을 이용해 해쉬값을 다음과 같이 다시 정의함 (int index = X.hashCode() % M)

- 여기서 M은 2의 지수승 형태임. 즉, M이 2^a 형태라면 hashCode()의 반환값에서 하위 a개의 비트만을 사용함

- 이러한 방식은 1/M 확률로 서로다른 해쉬 값을 갖는 객체들이 같은 index를 갖게하고 해쉬 충돌이 발생할 수 있음

- HashMap이 무조건 O(1) 이 아닌 이유는 해쉬 충돌이 발생했을 때 처리하기 위한 로직이 추가적으로 요구되기 때문(Separate Chaining)

 

HashMap에서 해쉬 충돌을 방지하기 위한 방법

- 위에서 2^32개의 데이터를 모두 담지 못한다는 문제로 hashCode()의 반환값을 M이라는 숫자로 나눈 나머지를 취했음

- 이러한 방식에서 발생할 수 있는 해쉬충돌을 해결하기 위한 방법으로 두 가지가 있음(Open Addressing, Separate Chaining)

- 해쉬 충돌이 발생한다면 HashMap을 O(1)이라고 할 수 없음

1. Open Addressing

- 데이터를 삽입하려는 해시 버킷이 이미 사용 중인 경우 다른 해시 버킷에 해당 데이터를 삽입하는 방식

 

1) Linear Probing

- 데이터를 저장/조회할 해쉬 버킷을 찾는 방식 중 하나

- Worst Case O(M)

 

https://medium.com/@matthewharrilal/open-addressing-resolving-collisions-one-day-at-a-time-49415ca73f71

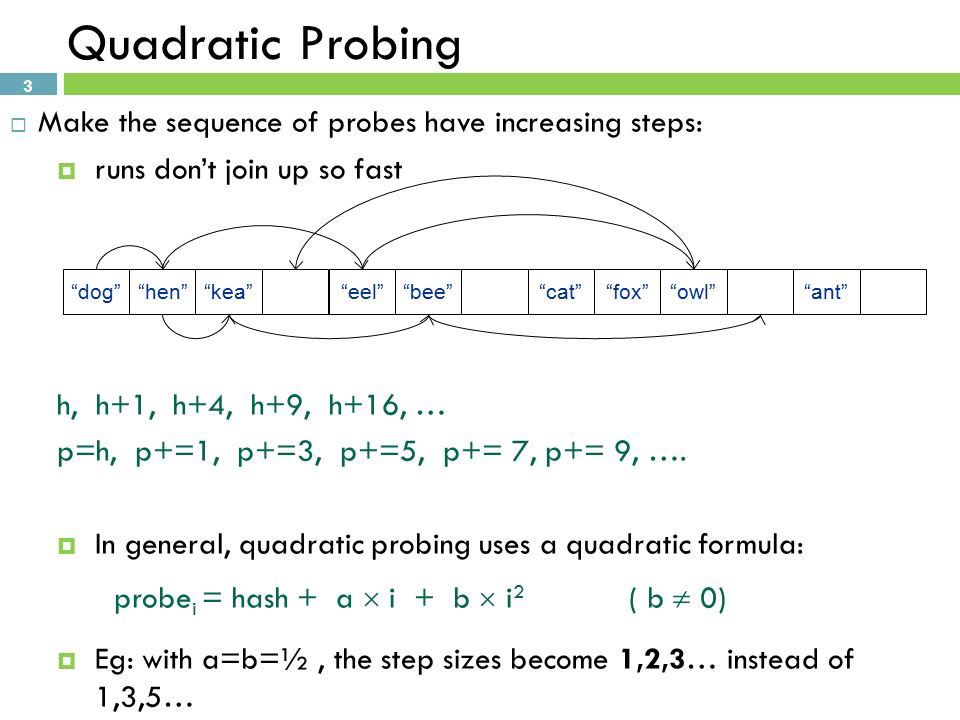
2) Quadratic Probing

- Worst Case O(M)

 

https://medium.com/@matthewharrilal/open-addressing-resolving-collisions-one-day-at-a-time-49415ca73f71

 

 

2. Separate Chaining **

- 각 배열의 인자(value)는 인덱스가 같은 해시 버킷을 연결한 링크드 리스트의 첫 부분(head)

- 동일  index(hashCode() % M)로 인해서 충돌이 발생하면 그 index가 가리키고 있는 LinkedList에 노드를 추가하여 값을 추가함

- 이렇게 함으로써 충돌이 발생하더라도 데이터를 삽입하는 데 문제가 없음.

- Java 8 이전에서는 LinkedList를 활용했고 Java 8이후부터는 'Red-Black Tree'를 이용함(버킷 데이터가 8개 이상인 경우에 해당)

- Java 8 이전 : Worst Case O(M)

- Java 8 이후 : O(logM)

 

https://www.researchgate.net/figure/Hash-table-representation-for-separate-chaining_fig2_284454241

 

Open Addressing 과 Separate Chaining의 차이

- 두 방식 모두 O(M) 이지만 Open Addressing의 경우 연속된 공간에 데이터를 저장하기 때문에 Separate Chaining에 비하여 캐시 효율이 높다

- 따라서 배열(HashMap의 key들)의 크기가 작다면 Open Addressing이 유리하지만 배열의 크기가 크다면 Separate Chaining가 유리함

- Open Addressing의 경우 데이터 삭제시에도 효율이 좋지 못함

- Java HashMap에서 사용하는 방식은 Separate Channing (+ 버킷 데이터가 8개 이상일때 부터 Red-BlackTree)

- Java HashMap에서 기본 버킷 개수(initial capacity)는 16이고 16개의 버킷에 데이터 개수가 모두 포화상태가 된다면 버킷 개수를 2배씩 늘린다.(최대 버킷 개수 2^30)

- 버킷 개수를 늘릴 때마다 Separate Chain을 재구성해야 하는 문제가 있음

- HashMap 객체에 저장될 데이터의 개수가 어느 정도인지 예측 가능한 경우에는 이를 생성자의 인자로 지정하면 불필요하게 Separate Chaining을 재구성하지 않게 할 수 있음

예시) new HashMap<String, Integer>(10); // 16개의 버킷 크기보다 불필요한 6개의 버킷을 생성하지 않음

 

cf. Tree와 LinkedList 차이

- Tree가 O(logN) 이지만 데이터 개수가 적다면 LinkedList와 크게 차이 없음

- LinedList 삽입 O(1), Tree 삽입 O(logN)

 

 

Separate Chaining의 문제점

- M은 hashCode()의 반환값이 int형(2^32)을 모두 포함하기 위해 2^a 형태로 표현됨(32비트 영역을 고르게 사용되게 하기 위함)

- M은 2^a 형태로 표현된다는 것은 haschCode() % M이 hashCode()의 하위 a개의 비트만을 사용한다는 것을 의미함

- 그렇기 때문에 해시 값을 2의 승수로 나누면 해시 충돌이 쉽게 발생할 수 있음 (M값이 작을 수록 충돌은 더욱 자주 발생)

- 즉, 모든 key의 hshCode() 값에서 하위 a개의 비트가 같다면 같은 해쉬 버킷에만 저장될 것

- 이러한 문제점을 해결하기 위해 '보조 해쉬 함수(supplement hash function)'가 등장

 

 

보조 해쉬 함수

-  보조 해쉬 함수의 목적은 'key'의 해쉬 값을 변형하여, 해시 충돌 가능성을 줄이는 것

- 아래는 Java 8에서의 HashMap 보조 해쉬 함수

static final int hash(Object key) { 
	int h; 
	return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); 
}

- 위 보조 해쉬 함수는 상위 16비트를 XOR 연산하는 간단한 형태이다.

- 위에서 볼 수 있듯이 보조 해쉬 함수는 key의 해쉬 값 자체를 변형시킴으로써 해쉬충돌을 처리한다.

 

---

String의 해쉬 값

- 기본적으로 Integer, Long, Double 같은 Number 객체는 값 자체를 해시 값으로 사용하기 때문에 충돌이 없는 완전한 해시 함수 대상으로 만들 수 있음

- 하지만 String을 포함한 다른 객체들에 대해서는 완벽한 해쉬 값을 만들 수 없음(충돌이 발생함)

 

- Java 8에서의 String의 hashCode()

public int hashCode() {  
        int h = hash;
        if (h == 0 && value.length > 0) {
            char val[] = value;

            for (int i = 0; i < value.length; i++) {
                h = 31 * h + val[i];
            }
            hash = h;
        }
        return h;
}

- 위 String의 hashCode()는 다항식을 쉽게 계산하는 로직임

- h가 계산하고자 하는 해쉬 값임

- 참고 : https://jh-labs.tistory.com/15

 

https://nesoy.github.io/articles/2018-06/Java-equals-hashcode

- 위에서 볼 수 있듯이 String의 해쉬 값은 각 요소의 값에 31의 인덱스 역순의 승수를 곱한 형태를 모두 더한 값이다.

- String이 String Constant Pool에 존재하지 않는다면 String의 해쉬 값을 계산해야하는 오버헤드가 있음.

 

 

[String의 hashCode()에서 31을 사용한 이유]

- 31은 소수이면서 홀수임

- 2^n을 곱했다면 n비트만큼 shift 연산을 하기 때문에 새로 채워진 비트 값이 모두 0으로 될 것(충돌 가능성이 높아짐)

- 소수를 곱한 이유는 아직 모름

 

Reference

- https://d2.naver.com/helloworld/831311