티스토리 뷰
Balanced Tree
- 한쪽으로 노드가 몰리는 Binary Search Tree의 단점을 보완하고자 등장
- DBMS에서 가장 범용적으로 사용되는 자료구조
- Binary Search Tree와 유사하지만 depth를 자동으로 잡아주기 때문에 탐색 시간복잡도가 O(logN)을 보장함
- 하지만 depth에 영향을 줄 수 있는 insert, delete 경우에 대해서는 성능이 좋지 않을 수 있음
- 결론적으로, 데이터를 얼마나 자주 삽입, 삭제할 것인가에 따라서 B-Tree Index를 활용할지 말지를 결정
- 즉, 갱신 빈도가 높은 테이블에 인덱스를 지정할 경우, 인덱스 재구성 발생 빈도가 높아진다는 점을 고려해야 함
B-Tree
- 하나의 노드에 여러개의 값이 배치되는 구조의 트리
- 차수 M의 B Tree는 하나의 노드에서 최대 M개의 자식 노드를 가질 수 있음을 의미함
- DBMS, 파일 시스템에서 많이 사용됨
- 대량의 데이터를 다룰 때, 하나의 노드에 여러 개의 데이터를 담을 수 있으므로 유리함(depth가 줄어듬)
- 파일시스템에서 블록단위로 노드를 구성하면 더욱 효율적인 데이터 관리 가능
- 데이터가 항상 "정렬된 상태로 유지"된다는 것이 핵심(자식 노드의 범위를 지정할 수 있기 때문)
- Binary Search Tree와 유사하지만, 한 노드 당 자식 노드가 2개 이상 가능
- B-Tree는 Balanced Tree이다. (즉, 삽입, 삭제시 인덱스 재구성 발생 가능)
- 데이터 삽입은 leaf node에만 발생하고 노드가 모두 찰 경우 depth가 커지는 방식으로 트리가 구성됨
- 인덱스를 구성하는 컬럼의 카디널리티가 높은 경우(중복된 값의 row가 적은 경우) 적합
- 기본적을 인덱스의 키는 16KB이다
[탐색]
- 시간복잡도 : O(logN)
- 이진탐색트리와 유사하게 root node부터 시작해 자식 노드의 개수만큼 decision과정을 거친다.
- 매 단계에서 모든 노드에는 데이터들이 정렬되어 있고, 탐색할 키값과 일치한 지 검사한다.
- 찾고자하는 키 값이 현재 노드의 키값보다 작을 경우, 왼쪽 서브 트리로 내려간다.
- 반대로 찾고자하는 키 값이 현재 노드의 키값보다 클 경우, 현재 노드의 다음 키값보다 작은 노드로 이동한다.
[삽입]
- B-Tree에서 Insertion의 경우, 새로운 노드는 반드시 leaf node에만 추가될 수 있음
- 삽입시 먼저 트리가 비어있는지 확인한다.
- 비어있지 않을 경우, 새로 추가될 key-value는 이진탐색트리와 같은 방식으로 위치를 찾는다.
- 삽입될 key-value가 들어갈 leaf node를 찾고 해당 노드 안에서 key값의 '오름차순'으로 저장된다.
- 만약 삽입될 leaf node에 데이터가 모두 차있다면, 해당 노드에서 중앙값을 기준으로 두 개로 나누며 중앙값을 부모 노드로 보낸다.
- 만약 두 개로 나누는 과정이 루트노드에서 발생된다면 루트 노드의 가운데 값을 새로운 루트 노드로 하고 나머지를 절반으로 나눈다. 그리고 트리의 높이는 1 증가한다.
예시 1) 루트 노드가 split 되어 트리 높이가 1 증가하는 경우
- B-Tree of Order 3 : 최대 가질 수 있는 자식 노드 개수 3
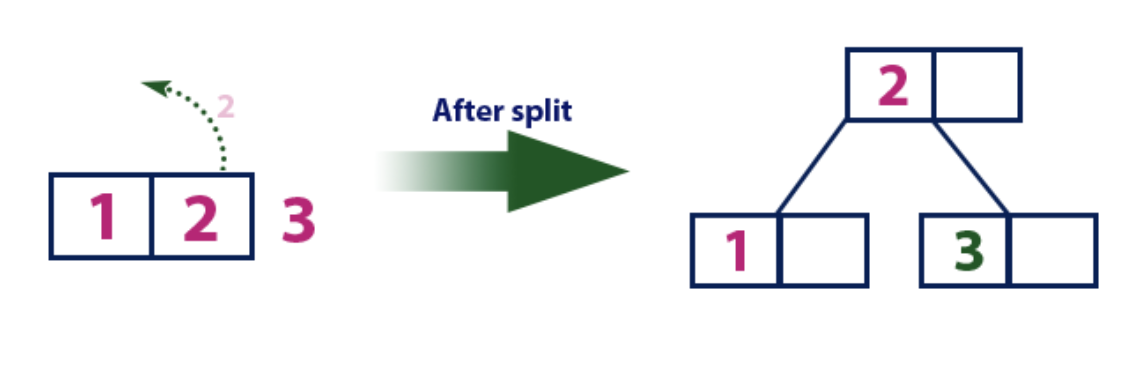
예시 2) leaf node가 무도 차있어서 split이 발생하는 경우
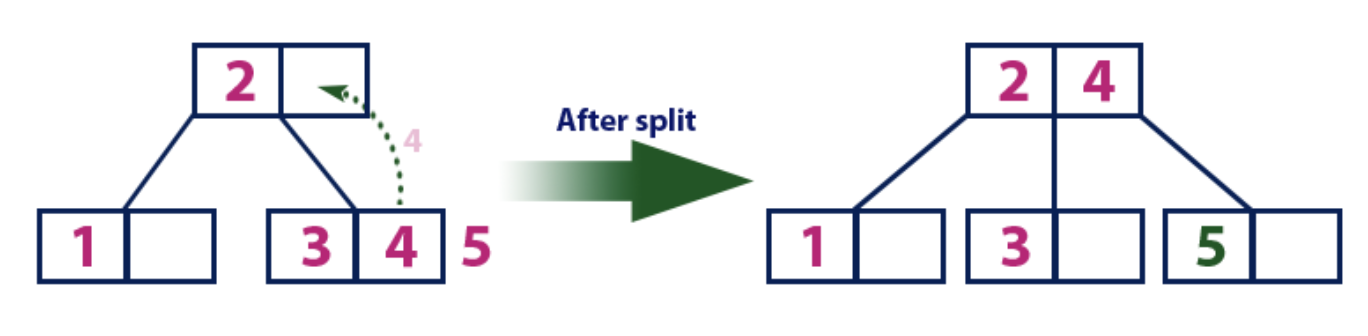
- 새로 삽입될 key값 5는 2보다 크기 때문에 두 번째 자식 노드로 내려온다.
- 이때, 해당 leaf node가 모두 차 있기 때문에 split이 발생한다.
- leaf node에서 3, 4, 5 중 middle 값인 4를 기준으로 split 하고 4를 부모 노드로 올린다.
- 부모 노드에 빈공간이 있으므로 4가 저장된다.
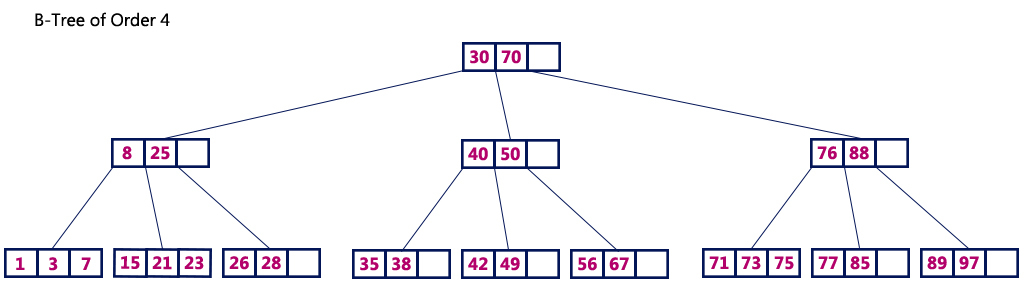
B+Tree
- MySQL의 DB engine인 InnoDB는 B+tree로 이뤄져 있으며 이는 B-tree에서 확장된 개념
- 비단말 노드(not leaf node)는 인덱스 역할만 하고 leaf 노드는 순차 데이터 부분을 담당함
- 인덱스 부분의 key 값은 leaf에 있는 key 값을 직접 찾아가는 데 사용
- leaf 노드끼리 연결 리스트로 연결되어 있어서 범위 탐색에 매우 유리
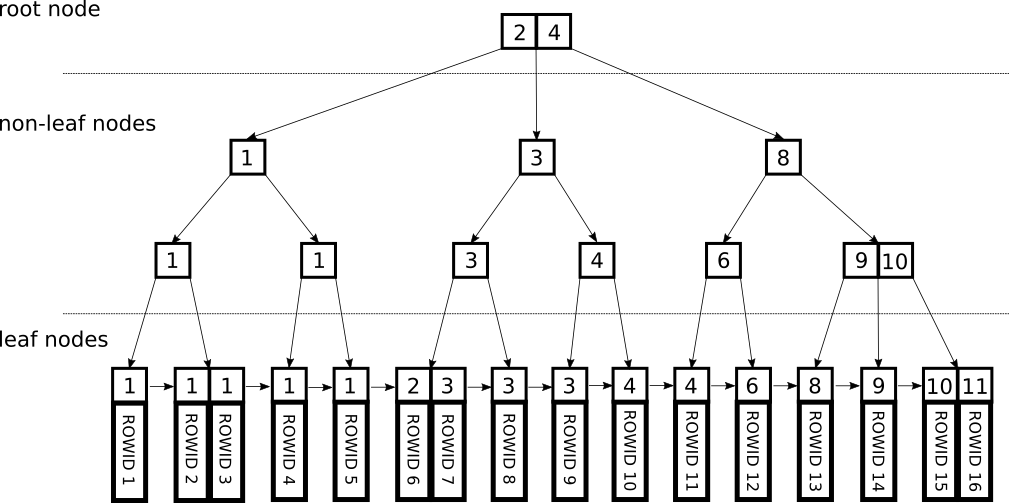
인덱스를 B Tree로 구성하는 이유
- 일반적인 트리는 포인터 계산에 필요한 물리적 시간이 B Tree보다 비효율적
- B Tree는 일반 이진탐색트리가 아니라 Balanced tree라는 점에서 O(logN)을 보장하지만 삽입, 삭제시에 트리구조가 변경될 수도 있음
- 해쉬테이블의 경우 정렬이 없기 때문에 범위 탐색에 비효율적
- 배열의 경우 (정렬되어 있다면) 탐색은 좋지만, 삽입이나, 삭제를 할 경우에는 O(n) 이기 때문에 비효율적
- 배열의 경우 삭제 및 중간 삽입 시 n개의 데이터를 이동시켜야 한다는 단점이 있으므로 비효율적
- B Tree는 하나의 노드에 데이터들을 "정렬"된 배열처럼 구성할 수 있기 때문에 참조포인터가 적어 빠르게 메모리 접근 가능(contiguous)
- B Tree는 트리 내 모든 데이터가 "항상 정렬된 상태로 유지"되기 때문에 조건 쿼리에서 =, >, < 등의 범위탐색에도 효율적
- 탐색보다는 좋지 못하지만, 삭제, 삽입의 경우에도 대개 O(logN)의 시간복잡도를 가짐
cf. 데이터베이스 인덱스 종류 -> https://jh-labs.tistory.com/172
Reference
- https://helloinyong.tistory.com/296
- https://zorba91.tistory.com/293
- http://www.btechsmartclass.com/data_structures/b-trees.html
- https://www.qwertee.io/blog/postgresql-b-tree-index-explained-part-1/
- https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html
'[ Basic ] > # 데이터베이스' 카테고리의 다른 글
| [DB] Clustered / Non-Clustered Index (0) | 2022.05.31 |
|---|---|
| <추천글>[DB] Index 종류와 카디널리티 (0) | 2022.01.11 |
| [DB] Index 적용 및 성능분석, 실행계획 분석 (0) | 2021.12.16 |
| <추천글>[DB] Transaction의 Isolation level을 나눠 둔 이유 (0) | 2021.11.29 |
| [DB] 실행계획 항목 분석 기초 (0) | 2021.10.13 |
- Total
- Today
- Yesterday
- argocd
- K8s
- LFCS
- 컨트롤러
- go
- docker
- 코틀린
- ubuntu
- ci/cd
- CICD
- Kubernetes
- spring
- kafka
- GitOps
- Linux
- db
- golang
- RDB
- 쿠버네티스
- github actions
- container
- 카프카
- jvm
- Controller
- Java
- 우분투
- rolling update
- Stream
- Non-Blocking
- helm
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
